There is an assignment that starts with these notes. Click here for the LaTeX used to typeset the assignment.
Puzzle games, solutions, and state diagrams
If you haven't noticed this yet in your math-based courses, one of the quirks of an abstract mathematical definition is that it can apply to really unexpected examples. Part of the fun of theoretical computer science is that those abstract mathematical definitions are often not too hard to reverse engineer from the unexpected examples. Case in point, let's play some puzzle games, shall we?
Some 2-D Puzzle Games
Directional Mazes
- An \(n\times m\) grid \(G\) of positions, where \(n\) and \(m\) are whole numbers
- A set of legal positions \(L \subseteq G\)
- Two postions called \(S\)tart and \(E\)nd
- A set of legal moves \(A \subseteq \{\Uparrow, \Downarrow, \Rightarrow, \Leftarrow\}\)
- A spelunker, \(C\)oby, that inhabits any legal position
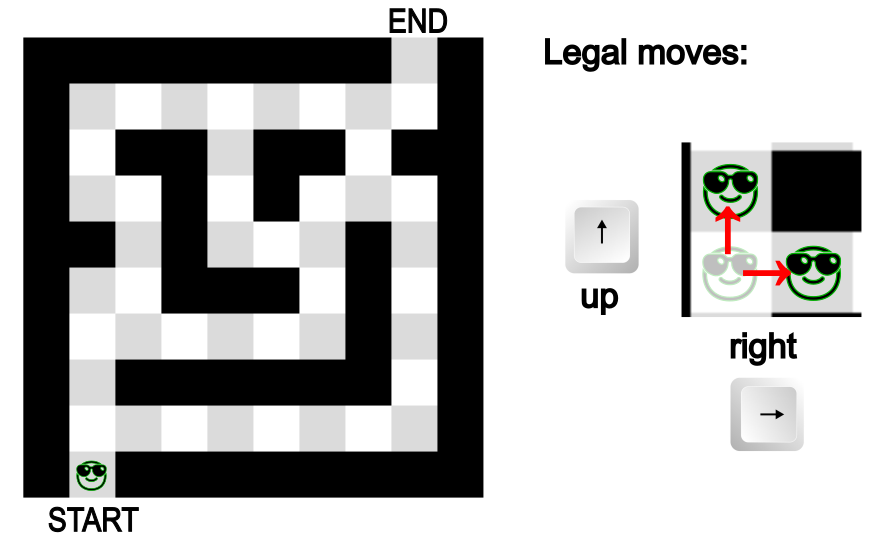 The Smiley Maze
The Smiley Maze
The directional maze above consists of a \(10\times 10\) grid of positions. The set of legal positions \(L\) is the set of white or beige positions, and in this case the only legal moves are \(A = \{\Rightarrow, \Uparrow\}\).
Note. We assume throughout this section that attempting a move from a legal position to a non-legal position ends the game.
- Does the sequence \(\Uparrow\Uparrow\Uparrow\Rightarrow\Uparrow\) solve the Smiley Maze?
- Find a solution to the Smiley Maze, in the form of a sequence of legal moves from \(A\).
- How many solutions are there?
- Change one position on the grid from illegal to legal such that there is exactly one additional solution after the change.
 The Spotted Maze. The \(S\)tart is in the bottom-left corner and the \(E\)nd is in the top right.
The Spotted Maze. The \(S\)tart is in the bottom-left corner and the \(E\)nd is in the top right.
So, we have already seen that a solution is a sequence of legal moves that brings \(C\)oby from the \(S\)tart to the \(E\)nd of the maze. We have already seen that more than one solution can exist for a particular maze.
Sokoban games
Sokoban is a puzzle videogame developed by Thinking Rabbit in the 1980s. The format of the game is very similar to a directional maze: you control a character by instructing them to perform one of four legal moves \(\{\Uparrow, \Rightarrow, \Leftarrow, \Downarrow\}\) to move from one legal position to another. The difference is an added element: there are boxes you have to push into certain finishing positions. It's a little easier to understand the game once you've played it a bit.
We are always going to assume that the set of legal moves in a Sokoban game is \(A = \{\Uparrow, \Rightarrow, \Leftarrow, \Downarrow\}\). Similar to the situation in a directional maze, a solution is a sequence of legal moves that put boxes over all of the finishing positions (the red dots). In this case, the starting configuration of the game really matters!
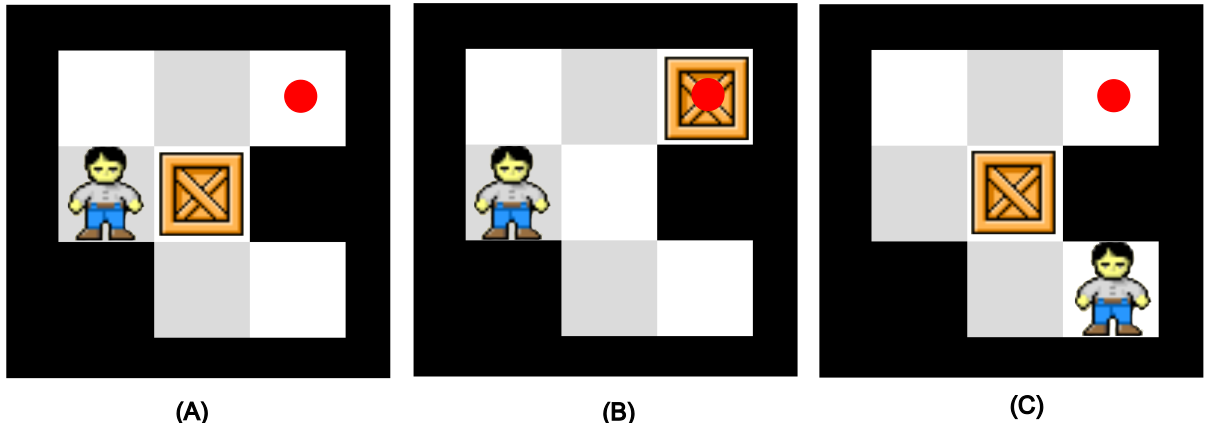 Three more (smaller) Sokoban games, (A), (B), and (C).
Three more (smaller) Sokoban games, (A), (B), and (C).
State Diagrams
In directional mazes and Sokoban games, hitting the arrow keys is what allows us to transform one configuration of the game board into another. The computer science words for configuration and transform are state and transition respectively.
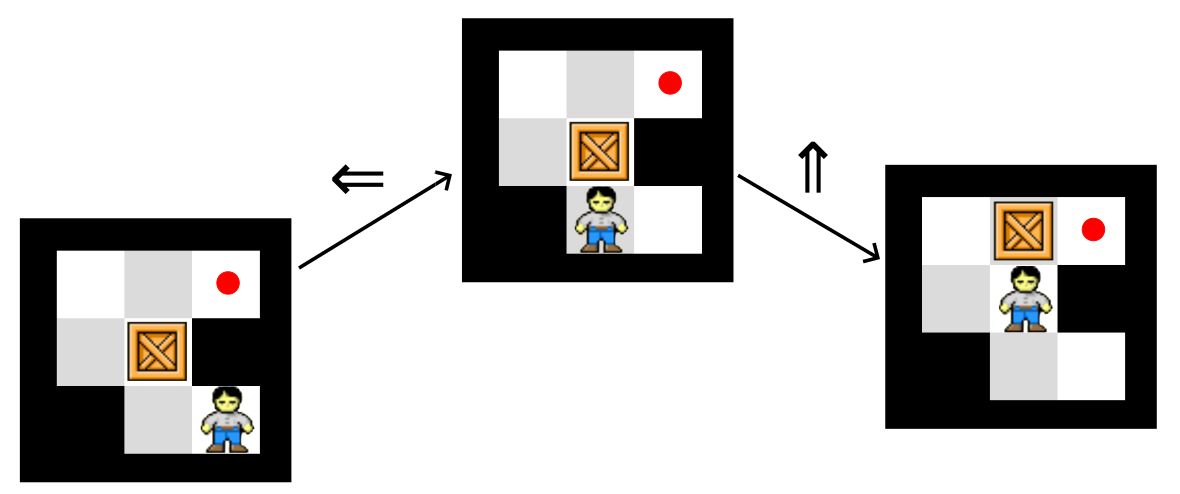 Two state transitions between three states \(s_0,s_1,s_2\), respectively, of of Sokoban game (A).
Written using the labelled-arrow notation \(s_0 \xrightarrow{\Leftarrow} s_1 \xrightarrow{\Uparrow} s_2\).
Two state transitions between three states \(s_0,s_1,s_2\), respectively, of of Sokoban game (A).
Written using the labelled-arrow notation \(s_0 \xrightarrow{\Leftarrow} s_1 \xrightarrow{\Uparrow} s_2\).
The picture above and your solution to the State and Transition exercise that came after it is what's called a state diagram. The state diagram with six states that you drew is not a complete state diagram, because not every state (and state transition) appears in it. These can be a bit difficult to draw usually, because even simple games can have very complex state diagrams.
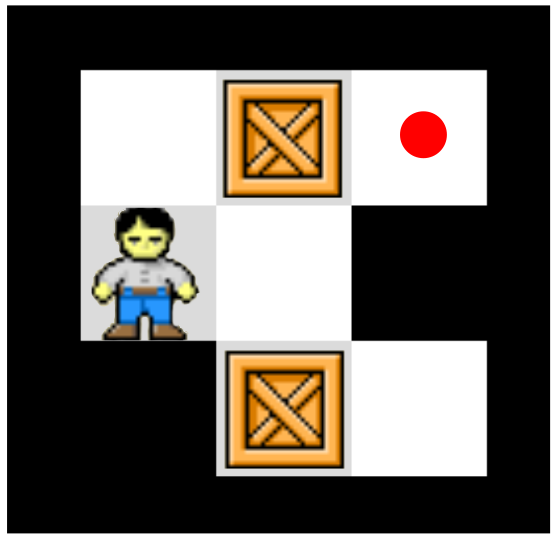 Sokoban game (D).
Sokoban game (D).
As you might have discovered already, state diagrams don't always need have the full configuration of the game drawn into every state. Forgetting about all of that extra information and just drawing little labelled circles for states (maybe the label describes the state a little bit) is a lot more convenient. A state diagram that doesn't have any description at all written into each state is called an abstract state diagram, because the precise nature of every state has been abstracted away.
Transition Tables
A more formal way of writing down a state diagram is a transition table. We will leave the formal definition for next time, when we start to treat state diagrams as formal entities called automata, but the basic idea should be intuitive. A transition table records all the state transitions in one big table. For example, the state diagram for abstract state diagram (A) is the table below:
| \(\textcolor{gray}{\rightarrow}\) | \(\Uparrow\) | \(\Rightarrow\) | \(\Downarrow\) | \(\Leftarrow\) |
| \(s_1\) | \(s_2\) | |||
| \(s_2\) | \(s_3\) | \(s_4\) | ||
| \(s_3\) | \(s_2\) | |||
| \(s_4\) | \(s_2\) |
In the left-most column of the table, you can see the states of the state diagram, and at the top (in the first row) you can see all the legal moves. If \(s\) is a state and \(a\) is a legal move, then if the \((s, a)\)-indexed item in the table is the state \(t\), then you should read: \(s \xrightarrow{a} t\). For example, in the transition table for abstract state diagram (A), you can see that the \((s_3,\Uparrow)\)-indexed item is \(s_2\), because \(s_3 \xrightarrow{\Uparrow} s_2\).