CSCI 341 Theory of Computation

Fall 2025, with Schmid

$\looparrowleft$ language acceptance finitely recognizable languages $\leadsto$

Finite and Infinite Automata

If you can write down the whole state diagram of an automaton, then we call it a finite automaton, because it has a finite number of states and transitions. If there are not finitely many states and transitions, then we call the automaton infinite. As we are about to see, there are some very natural examples of infinite automata!

By "natural", we mean something specific, actually: in the examples below, states are not "abstract" in the same way as we were writing before, when we wrote "$x_0$", or "$s_1$", or whatever. The states in the examples are little bit like the states of a puzzle game: they carry some concrete interpretation, and the same can be said about the transitions between these states. For a quick example, recall that the state of a maze is determined by the position of the player---the position is the semantics of the state. Then the transitions between the states are the moves the player was allowed to make---the allowable moves are the semantics of the transitions. (The word semantics is a fancy word for "meaning".)

(Money Bags) Consider the following (very silly) puzzle game, called Money Bags. You play the angel emoji collecting coins below: every time you land on the space with the money bag, you get $\$5$.

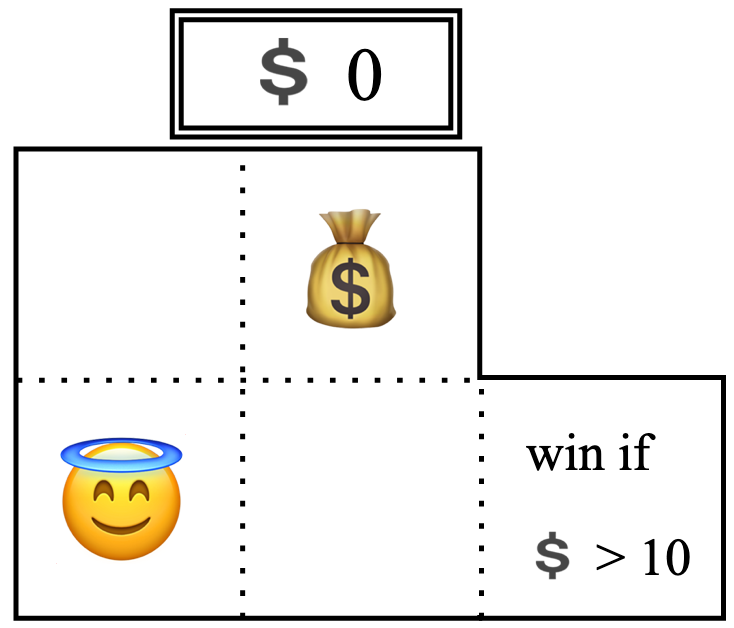A Money Bags puzzle.

What pieces of information constitute a state of this Money Bags? Which states are the winning states?
What does the state diagram of this game look like?

The next example is a bit more abstract, but the state diagram ends up being a lot simpler than the Money Bags state diagram.

(The Reverse Naturals) We are going to define an automaton $\mathcal A_{RNat} = (Q, A, \delta, F)$. The states of the Reverse Naturals automaton are the natural numbers, $Q = \mathbb{N} = \{0, 1, 2, 3, \dots\}$. We can already see that the automaton is infinite! The alphabet of input letters is only going to have one letter: $A = \{l\}$ ($l$ for "one $l$ess"). The transitions between the natural numbers are the result of subtracting one: \[ \delta = \big\{ (n + 1, l, n) \mid n \in \mathbb N \big\} \]

(Hey that's me!) What language does the number $1$ accept in the Reverse Naturals automaton? What language does the number $5$ accept in the Reverse Naturals automaton? Given any $n \in \mathbb N$, what language does the number $n$ accept in the Reverse Naturals automaton?

The Brzozowski Construction

We defined languages abstractly, as arbitrary sets of words from an alphabet. But then we talked about languages accepted by states of automata. Are these the same? In other words, is every language the language accepted by some automaton? As a matter of fact, the answer to this question is "yes"! And moreover, it just takes one automaton to see this in action. The automaton we are going to construct below is called the "Brzozowski automaton", and it is very infinite.

The basic idea is that the set of all languages is the state space of an automaton. That is, we are going to define an automaton whose states are languages (observe that these states have a semantics, just liike in the Reverse Naturals automaton!), and the transitions between states (i.e., languages) are Brzozowski derivatives, in the following sense.

(Brzozowski Derivatives) Let $A$ be a set of input letters and let $a \in L$. Given a language $L \subseteq A^*$, we define the $a$-derivative of $L$ to be the set \[ a^{-1} L = \big\{ w \in A^* \mid a\ w \in L \big\} \] In other words, $a^{-1} L$ is the set of words $w$ such that adding $a$ to the beginning of $w$ produces a word in $L$.

Remember that we want to define an automaton where the languages are the states. This means that we want to think of languages as programs (because they are states and states are programs). The program that corresponds to a language $L$ should really be thought of as "eating letters" as it runs, and accepting when it has nothing left to eat. In the simplest case, this is how you should imagine the $a$-derivative of just a word: $a^{-1}\{a\ b\ c\} = \{b\ c\}$. For arbitrary languages, taking the $a$-derivative is what is meant by "eating all the $a$'s".

(Where's the "b"?) What is the $b$-derivative of the language $\{a, aa, aaa\}$?

Ok, but what is the $a$-derivative of the word $a$ (of length $1$)? Well, remember that $a^{-1}aw = w$ for any word $w$. This includes the empty word, or $w = \varepsilon$, so \[ a^{-1}\{a\} = a^{-1}\{a\varepsilon\} = \{\varepsilon\} \]

(Where did the "$a$" go?) Calculate the language $a^{-1}\{a, aa, aaa\}$.

(More Practice with Derivatives) Compute the $a$-derivative, $b$-derivative, and $c$-derivative of the languages below:

$L_1 = \{\varepsilon, aa, ba, cab, c, acab\}$
$L_2 = \{aa, aaa, aaaa, caaa\}$
$L_3 = \{\varepsilon, bac, abc, cab\}$
$L_4 = \{b^n \mid n \in \mathbb N\}$ where $b^n = bbb\dots b$ is $n$ consecutive $b$'s
$L_5 = L_2 \cup L_3$
$L_6 = L_4 \cup \{a^n \mid n \in \mathbb N\}$

Alright, now that you've had some practice with derivatives, let's take a look at the formal definition of the Brzozowski automaton.

(The Brzozowski Automaton) The Brzozowski automaton is the automaton $\mathcal A_{Brz} = (2^{A^*}, A, \delta, F)$ where

$2^{A^*} = \{L \mid L \subseteq A^*\}$
$\delta = \{(L, a, a^{-1}L) \mid \text{\(a \in A$ and $L \subseteq A^*$}\} \subseteq 2^{A^*} \times A \times 2^{A^*}\)
$F = \{L \subseteq A^* \mid \varepsilon \in L\}$

In particular, the empty language $\emptyset \in 2^{A^*}$ is a state of the Brzozowski automaton.

(One at a Time) Consider the language $\{a, aa, aaa\}$. We see the following transitions in $\mathcal A_{Brz}$ with $A = \{a\}$:

(Basic Language Derivatives) What would the state diagram in One at a Time look like if $A = \{a, b\}$?

In the problem below, we are going to consider the states that are reachable from a given state. Formally, given states $x,y \in Q$ in an automaton $\mathcal A = (Q, A, \delta, F)$, $y$ is reachable from $x$ if there is a path \[ x \xrightarrow{a_1} x_1 \xrightarrow{a_2} x_2 \xrightarrow{a_3} \cdots \xrightarrow{a_k} y \] that starts at $x$ and ends at $y$.

(Unravelling a Finite Language) Draw a state diagram of all of the languages that are reachable from the language $L = \{\varepsilon, aa, ba, cab, c, acab\}$ in the Brzozowski automaton (by taking $a$- and $b$- and $c$-derivatives). Include all of the double-circles to indicate which languages are accepting states of the Brzozowski automaton. What language is accepted by $L$?

(Unravelling an Infinite Language) Draw a state diagram of all of the languages that are reachable from the language $L = \{(ab)^n \mid n \in \mathbb N\}$ in the Brzozowski automaton by taking $a$- and $b$-derivatives (the words in this language are $\varepsilon$, $ab$, $abab$, ...). Include all of the double-circled states to indicate which languages are accepting states of the Brzozowski automaton. What language is accepted by $L$?

What we are calling the "Brzozowski Fixed Point Theorem" below states that every language accepts itself in the Brzozowski automaton.

(Brzozowski Fixed Point) Let $\mathcal A_{Brz}$ be the Brzozowski automaton and let $L \in 2^{A^*}$ be a language/state of $\mathcal A_{Brz}$. Then $L = \mathcal L(\mathcal A_{Brz}, L)$.

We need to show two separate things: \[ \begin{aligned} \text{(1)} && L &\subseteq \mathcal L(\mathcal A_{Brz}, L) \\ \text{(2)} && L &\supseteq \mathcal L(\mathcal A_{Brz}, L) \end{aligned} \] We are going to show (1) here, and (2) you are going to prove in the problem below.

We are going to show that every word $w \in L$ is also an element of $\mathcal L(\mathcal A_{Brz}, L)$ (this is the definition of $\subseteq$). To paraphrase, we want to show that for any language $L \subseteq A^*$ and for any word $w \in A^*$, if $w \in L$, then $L$ accepts $w$ in $\mathcal A_{Brz}$. So, let's collect all of the words that satisfy this statement into their own language, \[ U = \{w \in A^* \mid \text{for any language $L \subseteq A^*$, if $w \in L$, then $L$ accepts $w$} \} \] We want to show that every word is in $U$, i.e., $U = A^*$. This is a situation where we can use Induction on Words!

In the base case, we want to show that $\varepsilon \in U$. So, let $L \subseteq A^*$ and suppose that $\varepsilon \in L$. We want to show that $\varepsilon \in \mathcal L(\mathcal A_{Brz}, L)$, which is to say that $L$ accepts $\varepsilon$. In the Brzozowski automaton, the accepting states (languages in $F$) are the languages that contain $\varepsilon$. Since we assumed that $\varepsilon \in L$, we know that $L \in F$, which tells us that $L$ accepts $\varepsilon$. By definition, $\varepsilon \in \mathcal L(\mathcal A_{Brz}, L)$. We have just shown that if $\varepsilon \in L$, then $\varepsilon \in \mathcal L(\mathcal A_{Brz}, L)$. By our definition of $U$, $\varepsilon \in U$. This concludes the base case of Induction on Words.

For the induction step, we are going to show that if $w \in U$ and $a \in A$, then $aw \in U$. This will allow us to conclude that $U = A^*$ by Induction on Words.

Let $w \in U$ and $a \in A$. Let $L \subseteq A^*$ and suppose that $aw \in L$. We want to show that $aw \in \mathcal L(\mathcal A_{Brz}, L)$, since this would tell us that $aw \in U$ like we wanted. Now, if $aw \in L$, then $w \in a^{-1}L$ by the definition of $a$-derivative. Since $w \in U$, we also know that $w \in \mathcal L(\mathcal A_{Brz}, a^{-1}L)$, i.e., $a^{-1}L$ accepts $w$. If we write $w$ as a sequence of letters $w = b_1b_2b_3\dots b_n$, then this means that there is a path \[ a^{-1}L \xrightarrow{b_1} L_1 \xrightarrow{b_2} \cdots \xrightarrow{b_n} L_n \qquad L_n \in F \] such that $L_n$ is an accepting state. But by definition of $\mathcal A_{Brz}$, $L \xrightarrow{a} a^{-1}L$, so actually we have a path \[ L \xrightarrow{a} a^{-1}L \xrightarrow{b_1} L_1 \xrightarrow{b_2} \cdots \xrightarrow{b_n} L_n \qquad L_n \in F \] This tells us that $L$ accepts $aw$, or equivalently, $aw \in \mathcal L(\mathcal A_{Brz}, L)$. We have just shown that if $aw \in L$, then $L$ accepts $aw$. By definition of $U$, this tells us $aw \in U$.

We have shown two things: that $\varepsilon \in U$, and if $w\in U$ and $a \in A$, then $aw \in U$. By Induction on words, $U = A^*$, or in other words, $L \subseteq \mathcal L(\mathcal A_{Brz}, L)$ for every language $L \subseteq A^*$.

(Language Determinism?) Is Brzozowski's automaton deterministic, total, or both?

(Cancelling Out) Let $L \subseteq A^*$ be a language.

Suppose that $\varepsilon \in a^{-1}L$. Name an element of $L$.
Suppose that $\varepsilon \in b^{-1}a^{-1}L$. Name an element of $L$.
Suppose that $c \in b^{-1}b^{-1}a^{-1}L$. Name an element of $L$.

To complete the problem mentioned in the proof of the Brzozowski Fixed Point Theorem, it helps to have the following lemma (lemma are like tiny theorems 🥺👉👈).

Let $w = a_1\cdots a_n$ and $u \in A^*$ be words in the alphabet $A$. If \[ u \in a_n^{-1}a_{n-1}^{-1} \cdots a_2^{-1} a_1^{-1}L \] then $wu \in L$.

Notice that $w$ has been reversed in the equation above.

This is a proof by ordinary induction on $n$.

In the base case, $n = 0$. Remember that the only word of length $0$ is $\varepsilon$. So, in the base case, we are trying to show that if $u \in L$, then $wu = \varepsilon u \in L$. But $\varepsilon u = u$, and we assumed at the beginning that $u \in L$. It follows that $wu \in L$.

For the induction step, let $w = a_1\cdots a_n a_{n+1}$ and assume the following induction hypothesis: for any $v\in A^*$, if $v \in a_{n}^{-1}a_{n-1}^{-1}\cdots a_{1}^{-1}L$, then $a_1\cdots a_nv \in L$. To start the induction step, suppose that \[ u \in a_{n+1}^{-1}a_{n}^{-1}\cdots a_{1}^{-1}L \] By definition of the Brzozowski derivative, \[ a_{n+1}u \in a_{n}^{-1}\cdots a_{1}^{-1}L \] Applying the the induction hypothesis with $v = a_{n+1}u$, we obtain \[\begin{aligned} wu &= a_1 \cdots a_n a_{n+1}u &&\text{($w = a_1 \cdots a_n a_{n+1}$)} \\ &= a_1 \cdots a_n v &&\text{($v = a_{n+1} u$)} \\ &\in L &&\text{(induction hypothesis)} \end{aligned}\] like we wanted.

(Language Accepts Itself) Let $L \subseteq A^*$ be any language. Prove that $\mathcal L(\mathcal A_{Brz}, L) \subseteq L$.

You do not need to use Induction on Words here. The statement you are trying to prove is equivalent to saying that if \[ L \xrightarrow{a_1} L_1 \xrightarrow{a_2} \cdots \xrightarrow{a_n} L_n \] and $\varepsilon \in L_n$, then $a_1a_2\cdots a_n \in L$. To see why this is true, write down a formula for $L_n$ in terms of $a_1,\dots,a_n$ and $L$ and use the lemma.

Top